Lattice learning 1

Preface

花了一下午的时间学完了线代
数学家们上辈子一定是天使吧，才能发明出这么美妙的东西
线性代数 相见恨晚

Chapter 1 The world of the Lattice

向量真是个神奇的东西，因为世界上的一切都可以用向量来表示。那么如果我们要去表示一个线性空间 $V$ ，我们就需要至少两个非线性相关的向量作为基底，比方说 $\vec{i}$ 和 $\vec{j}$，因此任意的一个向量都可以用基底的线性组合来表示出来，比如 $\vec{x}=a\cdot\vec{i}+b\cdot\vec{j}$ 。而能被 $\vec{i}$ 和 $\vec{j}$ 表示出来的所有向量的集合就称为这个线性空间 $V$ 。但是这里的’$a$’和’$b$’可以是任意的数字，那么如果我们假定这里的’$a$’和’$b$’都是整数（$a,b\in\mathbb{Z}$），这时我们就会得到一个整数格（Integer Lattice）。

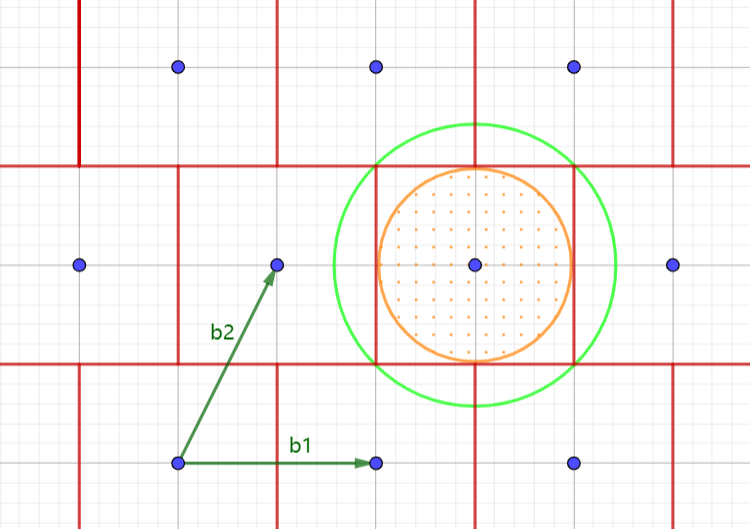
我们首先使得所有的向量起点都位于原点，此时，所有的向量都与它们各自的终点一一对应，也就是说，我们可以使用向量的终点来代替该向量。那么此时我们的整数格 $V$ 就会变成一群离散开来并且有序排布的点集。当然，这些点的排列方式并不唯一，可以通过一些简单的线性变换来得到一个新的格空间。

举个栗子吧，比方说我们现在有 $\vec{b_1},\vec{b_2},\cdots,\vec{b_n}$ 作为基，那么格空间里所有的向量都可以被看作是一个矩阵 $A$：
$$
A=\sum^n_{i=1}(b_i\cdot \mathbb{Z})
$$
当然你也可以把这些基看成一个矩阵 $B$：
$$
A=\sum^n_{i=1}(b_i\cdot\mathbb{Z})=B\cdot x(x\in\mathbb{Z}^n)
$$
所以说了这么多，格到底是什么东西？我们可以把它理解成一堆向量的集合，但是向量是很有意思的玩意。

Chapher 2 Notions in Lattice

行列式（Determinant）

一个矩阵的行列式可以看作是一种特殊的变换：它描述了由所有基向量组成的四边形或者多面体在这种线性变换中其面积或者体积的变化。

最短距离（Shortest distance）

比如一个由矩阵 $B$ 形成的格空间中，我们使用 $\lambda$ 来表示这个矩阵点集中的的最短距离，那么显然通过更换原点/基的方法来把这个问题变成一个 $SVP$：
$$
\lambda_1=min||x-y||\ \ \ (x,y\in B,x\not=y) \\
=min||x||\ \ \ (x\in B,x\not=\vec{0})~~~~~~
$$
另外，我们用 $\lambda_2,\lambda_3,\cdots,\lambda_i,\cdots,\lambda_n$ 来表示第 $i$ 短的距离，那么显然以下结论成立：
$$
\lambda_1\leq\lambda_2\leq\lambda_3\leq\cdots\leq\lambda_n
$$

Chapher 3 Problems in Lattice

最短向量 SVP (Shortest Vector Problem)

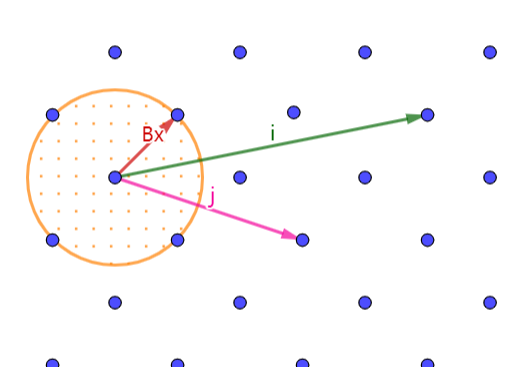
我们来考虑一个由矩阵 $B$ 构成的格空间 $L$ ，在其中去找这样的一个向量 $\vec{x}$ 满足：
$$
||B\vec{x}||= \lambda_1\ \ \ (x\in \mathbb{Z}^k)
$$

好像看起来不难？但是当我们拿到一组较差的基时，此时的 $SVP$ 就很难求了，但是也有一种 $SVP$ 的简化版本 $SVP_\gamma$ 。在 $SVP_\gamma$ 中，我们只需要找到这样的向量 $\vec{x}$ 即可：
$$
||B\vec{x}||\leq \gamma\lambda_1\ \ \ (x\in \mathbb{Z}^k)
$$

最近向量 CVP (Closest Vector Problem)

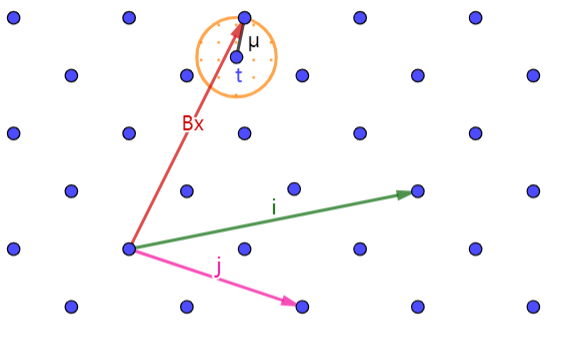
还是考虑一个由矩阵 $B$ 构成的格空间 $L$ ，给出一个点 $t$ ，在其中去找里点 $t$ 最近的一个向量 $\vec{x}$ ，也就是说：
$$
||B\vec{x}-\vec{t}||\leq\mu
$$

$CVP$ 也有它的简化版本 $CVP_\gamma$ ，其定义与 $SVP_\gamma$ 类似，即满足：
$$
||B\vec{x}-\vec{t}||\leq \gamma\mu\ \ \ (x\in \mathbb{Z}^k)
$$

$SVP$ 和 $CVP$ 都被证明是 np-hard 的问题 说白了就是难的离谱

Chapher 4 Geometric structure in Lattice

尝试解决CVP

CVP真的压根无法下手吗？显然不是。比如在笛卡尔坐标系里，只需要简单的上下取整就能找到此时的 $CVP$ ， $SVP$ 此时显然也是很简单的问题。那么我们只要能够将格 $\Lambda$ 变成一个几乎是正交基的格 $L$ ，那么我们就能很容易的解决 $SVP$ 和 $CVP$ 。我们通常称这个过程为’Lattice Basis Reduction’，比如’Gram-Schmidt’就是其中之一的方法，但是此时我们通过简单上下取整的操作不一定得到的就是正确的答案，也只有当 $||\vec{t}-\vec{v}||\leq min\frac{||\vec{b_i}||}{2}$ 时我们得到的才是正确的结果，原因如下图：