Summary of RSA Factorization Algorithm

爪巴了，数学知识它不进脑子啊

Pollard's p − 1

已知 $N=p\cdot q$ ，我们的任务是分解出其中的两个质因子

首先我们找到这样的一个 $L$ 满足 $L\mid p-1$ 且 $L\nmid q-1$ ，也就是存在整数 $i,j,k(k\neq0)$ 满足 $L=i\cdot (p-1)=j\cdot (q-1)+k$ ，由费马小定理可知
$$
a^L=a^{i\cdot (p-1)}=(a^{p-1})^i\equiv 1^i\ (mod\ p)\equiv 1\ (mod\ p)
$$
$$
a^L=a^{j\cdot (q-1)+k}=(a^{q-1})^i\cdot a^k\equiv 1^j\cdot a^k\ (mod\ q)\equiv a^k\ (mod\ q)
$$

所以 $p\mid a^L-1$ 而 $q\nmid a^L-1$ ，那么我们就可以得到 $p=gcd(a^L-a,N)$

听起来无比简单，但是，我们要如何找到这个 $L$ 呢？

在Pollard的观察中，如果 $p-1$ 恰好是许多小素数的乘积，所以我们可以利用 $p-1$ 的倍数 $n!$ （n不是非常大）来代替 $p-1$ ，即计算 $gcd(a^{n!}-1,N)$ （例如我们可以选择 $a=2$ ）

  • 如果结果是1，那就继续计算下一个 $n$
  • 如果结果是 $N$ ，那么可以尝试更换 $a$ 的值再次尝试
  • 如果结果是位于 $1$~$N$ 之间的一个数，那么这个数就是我们要找的 $p$

优化

  • 我们所要求的指一定是小于 $N$ 的，所以不用计算出 $a^{n!}-1$ 的确切值，中途膜 $N$ 即可
  • 我们上一步已经得到了 $a^{(n-1)!}$ 的值，所以继续计算 $a^{n!}=(a^{(n-1)!})^n$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
from gmpy2 import *

q = getPrime(64)
p = getPrime(64)
n = p * q
print(n)
print(p)
print(q)

sum = 2
for i in range(1,n):
    sum = pow(sum,i,n)
    # print(sum)
    if(gcd(sum-1,n)!=1):
        print(i)
        print(gcd(sum-1,n))
        break

当我们执行时，我们发现脚本只能有一定概率在有限时间内跑出结果，因为能够跑出结果的情况有且只有**$p-1$恰好是许多小素数的乘积**时，那么这样的分解方式需要多少时间呢？

这里贴一个书里的原图

22.png

Pollard’s ρ algorithm

波拉德的ρ算法是整数分解的一种算法，它只占用了很少的空间，并且它的预期运行时间与被分解的合数的最小质因数大小的平方根成正比

核心思想->生日悖论

​ 假设我们构造一个伪随机数列，比如说我们定义 $f(x)=x^2+1$ ，然后选择一个种子，比方说2，那么就可以得到 $x_1=f(2)$ 、 $x_2=f(f(2))$ 、 $x_3=f(f(f(2)))$ ……但由于生日悖论，这个伪随机数列总会的重复，而一旦重复，这个序列就会成为一个环，如下图，所以这种序列结构为这种算法得到了ρ算法这样的名字

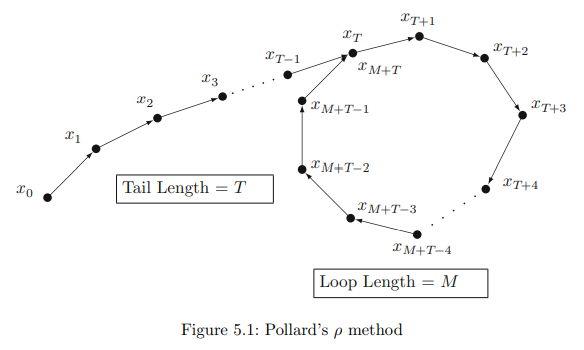
32.png

​ 那么现在我们要怎么利用这个序列来分解n呢？我们利用Floyd's cycle-finding algorithm发现：每次我们检查 $gcd(x_i-x_j,n)$ ，如果发现这个结果不等于1或n，那么这个结果就是n的非平凡因子了（即不等于1与n的因子），当 $x_i=x_j\pmod{p}$ 时，$x_i-x_j$ 必定存在p这个因子，而且我们注意到 $x_k\ mod\ p$ 这个序列也是重复的，也就是说，我们总能找到一组合法的(i,j)满足 $gcd(x_i-x_j,n)\neq1$ ，如果结果等于n时，也就代表Pollard's ρ algorithm失败了，但我们可以重新选择一组序列来进行计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import isPrime
from gmpy2 import gcd

n = xxxxxxxxxxxxxxxxxxxxxxxxxxxxxx

def maps(x,n):
    return (x * x + 1) % n

def pollard_rho(seed,n):
    anslist = []
    x2 = x1 = seed
    while True:
        x1 = maps(x1,n)
        x2 = maps(maps(x2,n),n)
        data = gcd(x1-x2,n)
        if(data != 1):
            return int(data)

def pollard_rho_Factor(n):
    ans = []
    while True:
        data = pollard_rho(2,n)
        ans.append(data)
        n = n // data
        if(n == 1):
            return ans
        if(isPrime(n)):
            ans.append(n)
            return ans

print(pollard_rho_Factor(n))

优化

​ 使用Brent's cycle finding method来取代Floyd's cycle-finding algorithm，其不同点就是从一步一检查变成了百步一检查，它定义 $z=(x_2-x_3)(x_3-x_5)(x_4-x_7)\cdots(x_{101}-c_{201})\pmod{n}$ 随后再检查 $gcd(z,n)$ 是否为1，这样的做法只是为了加速，但对于部分情况会失灵，比如当n是一个完全平方数时，是无法分解的，但也并不是没有办法，我们使用原本的正常方法即可